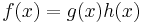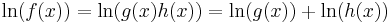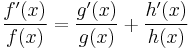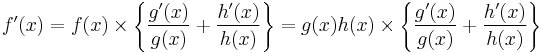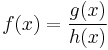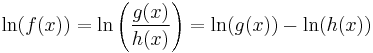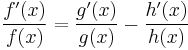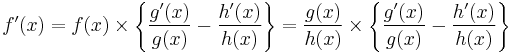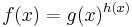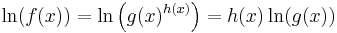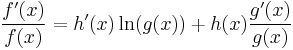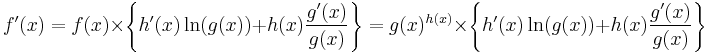Logarithmic differentiation
In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the logarithmic derivative of a function ƒ,[1]
The technique is often performed in cases where it is easier to differentiate the logarithm of a function rather than the function itself. Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or logarithmic to the base e) to transform products into sums and divisions into subtractions, and can also applied to functions raised to the power of variables or functions.[2][3] However, the principle can be implemented, at least in part, in the differentiation of almost all differentiable functions, providing that these functions are non-zero.
Contents |
Overview
For a function
logarithmic differentiation typically begins by taking the natural logarithm, or the logarithm to the base e, on both sides, remembering to take absolute values[4]
After implicit differentiation[5]
Multiplication by y is then done to eliminate 1/y and leave only dy/dx on the left:
The method is used because the properties of logarithms provide avenues to quickly simplify complicated functions to be differentiated.[6] These properties can be manipulated after the taking of natural logarithms on both sides and before the preliminary differentiation. The most commonly used logarithm laws:[3]
General case
Using capital pi notation,
Application of natural logarithms results in (with capital sigma notation)
and after differentiation,
Rearrange to get the derivative of the original function,
Applications
Products
A natural logarithm is applied to a product of two functions
to transform the product into a sum
Differentiate by applying the chain and the sum rules
and, after rearranging, get[7]
Quotients
A natural logarithm is applied to a quotient of two functions
to transform the division into a subtraction
Differentiate by applying the chain and the sum rules
and, after rearranging, get
After multiplying out and using the common denominator formula the result is the same as if after applying the quotient rule directly to  .
.
Composite exponent
For a function of the form
The natural logarithm transforms the exponentiation into a product
Differentiate by applying the chain and the product rules
and, after rearranging, get
See also
Calculus/More Differentiation Rules#Logarithmic differentiation at Wikibooks: see for textbook examples of logarithmic differentiation.: see for textbook examples of logarithmic differentiation.
- Darboux derivative, Maurer–Cartan form for generalizations to arbitrary Lie groups
- List of logarithm topics
- List of logarithmic identities
Notes
- ^ Krantz, Steven G. (2003). Calculus demystified. McGraw-Hill Professional. pp. 170. ISBN 0071393080.
- ^ N.P. Bali (2005). Golden Differential Calculus. Firewall Media. pp. 282. ISBN 8170081521.
- ^ a b Bird, John (2006). Higher Engineering Mathematics. Newnes. pp. 324. ISBN 0750681527.
- ^ Dowling, Edward T. (1990). Schaum's Outline of Theory and Problems of Calculus for Business, Economics, and the Social Sciences. McGraw-Hill Professional. pp. 160. ISBN 0070176736.
- ^ Hirst, Keith (2006). Calculus of One Variable. Birkhäuser. pp. 97. ISBN 1852339403.
- ^ Blank, Brian E. (2006). Calculus, single variable. Springer. pp. 457. ISBN 1931914591.
- ^ Williamson, Benjamin (2008). An Elementary Treatise on the Differential Calculus. BiblioBazaar, LLC. pp. 25–26. ISBN 0559475772.
External links
- "Differentiation by taking logarithms – Teach yourself". mathcentre.ac.uk. http://www.mathcentre.ac.uk/students/topics/differentiation/by-logs/. Retrieved 2012-01-03.
- "Logarithmic differentiation". http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/logdiffdirectory/LogDiff.html. Retrieved 2009-03-10.
- "Calculus I – Logarithmic differentiation". http://tutorial.math.lamar.edu/Classes/CalcI/LogDiff.aspx. Retrieved 2009-03-10.
![[\ln(f)]' = \frac{f'}{f}](/2012-wikipedia_en_all_nopic_01_2012/I/fafa09bb6af098056c247ab5177217e6.png)
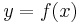
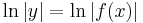
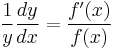
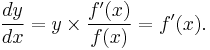
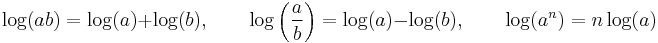
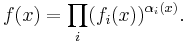
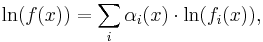
![\frac{f'(x)}{f(x)}=\sum_i\left[\alpha_i'(x)\cdot \ln(f_i(x))%2B\alpha_i(x)\cdot \frac{f_i'(x)}{f_i(x)}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/9815aa41a8f76a4a842b9983fc537ce2.png)
![f'(x)=\overbrace{\prod_i(f_i(x))^{\alpha_i(x)}}^{f(x)}\times\overbrace{\sum_i\left\{\alpha_i'(x)\cdot \ln(f_i(x))%2B\alpha_i(x)\cdot \frac{f_i'(x)}{f_i(x)}\right\}}^{[\ln (f(x))]'}](/2012-wikipedia_en_all_nopic_01_2012/I/35b442a08a67591bdfefd331b6fb0c15.png)